Messages/Notifications
-
No notifications yet.
Further Integration (videos, notes, quizzes with correction) - Welcome To Class
Further Integration (videos, notes, quizzes with correction): Introduction Topics
-
1 - Welcome To Class
: 0:03:44 mins
-
2 - Presentation of Objectives
: 0:05:36 mins
View PDF Notes
Take Quiz
-
1 - Presentation of Objectives
: 0:05:36 mins
-
2 - INTRODUCTION AND RECALLS OF BASIC INTEGRALS
: 0:19:41 mins
-
3 - 3-BASIC INTEGRALS (PART2)
: 0:07:38 mins
-
4 - BASIC INTEGRATION TECHNIQUES-INTEGRATION BY PARTS
: 0:18:58 mins
-
5 - BASIC INTEGRATION TECHNIQUES -SUBSTITUTION METHOD (PART 1)
: 0:07:15 mins
-
6 - BASIC INTEGRATION TECHNIQUES- SUBSTITUTION METHOD (PART2)
: 0:05:51 mins
-
7 - GCE TYPE QUESTIONS (JUNE 2020 QUESTION 3)
: 0:17:43 mins
-
8 - GCE TYPE QUESTIONS (JUNE 2018 QUESTION 4)
: 0:11:40 mins
-
9 - GCE TYPE QUESTIONS (JUNE 2018 QUESTION 4 part 2)
: 0:13:47 mins
View PDF Notes
Take Quiz
Introduction
Lessons: Further Integration
Good morning sir. Please sir can you afford for the solution of June 2021 paper3 Further Mathematics. VERY IMPOTTANT.
Please I need help
Please I have a problem on series and sequence
Please I have a problem on series and sequence
question 31 june 2020 has a problem, it is not showing
Thanks for th update lynn, did you propose something with respect to it????
Take note
Kernel:
It is a vector that maps unto the zero vector under the transformation. It is otherwise called the nulls space of the transformation. Let's consider an example below.... Find the kernel of the transformation T whose matrix is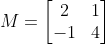
Solution
Let the kernel be the vector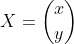
. Then we have that
Hence&space;=&space;\binom{0}{0} "X = ker(T) = \binom{0}{0}")
Sir can you explain to me the concept of kernel and image in transformation
Hello boul Paul. Be patient, your explanation is coming