TEFA: GCE A/L

March 22, 2021, 8:53 a.m.
Kemba
help 2 and 3

0

Reply
- March 22, 2021, 11:54 a.m.
  KENG ELSON MNKONG
  Hello kemba Ur solution will be ready by 6pm. Thanks
  
  0
March 18, 2021, 5:07 p.m.
KENG ElSON
good luck foir maths

0

Reply
March 14, 2021, 9:05 p.m.
KENG ELSON MNKONG
revise for the mock with this question

0

Reply
Feb. 27, 2021, 9:51 a.m.
Wanyu
Question 12

The horizontal distance between two men P and Q is 6 m. A ball is projected by P to Q with an initial speed of 10 ms^-1. Q catches the ball at a point vertically above him and at a height 3 m above the point of projection. Show that there are two possible angles of projection and find the time of flight in eac case (take g as 10 ms^-2).

Solution

Diagramatic interpretation

Showing that there are two possible angles of projection

At point A where Q catches the ball,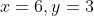 $x=6,y=3$

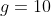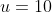Substituting in the above equation $g=10$ and $u=10$ we have:

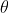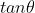For us to have two values of the projection angle $\theta$ , we must have two values for $tan \theta$ .

For us to have two values of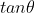 $tan\theta$ , the above quadratic equation in 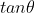$tan\theta$ must have two real and distinct roots. In other terms, the discriminant must be strictly positive

Therefore, for two angles of projection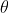 $\theta$ to exist, the discriminant of the above equation must be strictly positive.

Discriminant,

Since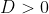 $D> 0$ , there exist two possible angles of projection.

Finding the time of flight in each case

The solution of the above equation in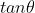 $tan \theta$ is given by:

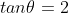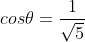
Using $tan\theta =2$ , $cos\theta =\frac{1}{\sqrt{5}}$

Substituting in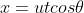 $x=utcos\theta$ above we have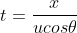 $t=\frac{x}{ucos\theta }$

So time of flight in seconds in this case is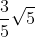 $\frac{3}{5}\sqrt{5}$

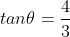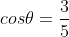
Using $tan\theta =\frac{4}{3}$ , $cos \theta =\frac{3}{5}$

Substituting in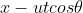 $x-utcos\theta$ above, we have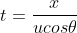 $t=\frac{x}{ucos\theta }$

So time of flight in seconds in this this case is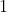 $1$

0

Reply
Feb. 25, 2021, 4:37 p.m.
Kemba
pleasw help number 13 and 12

0

Reply
- Feb. 27, 2021, 7:19 a.m.
  zozo
  Helloooooooo Good morning and hope you are doing well this is really a very long question to answer here may I know exactly the difficulties you face answering the questions or if you can snap what you tried doing so that we point out the mistakes it will be great
  
  0
- Feb. 27, 2021, 9:20 a.m.
  Wanyu
  Follow the solution above
  
  0
Feb. 23, 2021, 8:55 p.m.
Wanyu
Any question and submit

0

Reply
Feb. 16, 2021, 9:25 p.m.
Phanuelex
A smooth sphere A of mass 3m is moving with speed 5U on a smooth floor. It's collides directly with another sphere 3U. Given that the coefficient of friction is ¼

Find

A. Velocity of the spheres after impact

B. The loss in K.E due to the impact

0

Reply
- Feb. 17, 2021, 10:07 a.m.
  Kenyui
  actually the question lack enough information like: mass of the sphere with speed 3u was the sphere with speed 3u was moving in which direction?
  
  0
Feb. 14, 2021, 7:48 p.m.
Kenyui
trig tutorials

0

Reply