Messages/Notifications
-
No notifications yet.
June 2020 Paper 2 GCE A/L Pure Mathematics with Mechanics - Introductory video
June 2020 Paper 2 GCE A/L Pure Mathematics with Mechanics: Introduction Topics
-
1 - Introductory video
: 0:01:19 mins
-
2 - question1( part i: recalls)
: 0:03:48 mins
-
4 - question 1( solution to 1-ii)
: 0:12:56 mins
-
20 - question5 (solution to question 5a)
: 0:15:08 mins
-
23 - question5 (solution to question 5b part 2)
: 0:10:21 mins
View PDF Notes
Take Quiz
-
1 - introduction
: 0:01:19 mins
-
2 - question1(recalls on part i)
: 0:03:48 mins
-
3 - question1( solution to 1-i)
: 0:04:02 mins
-
4 - question1( recalls on part 1-ii)
: 0:17:09 mins
-
5 - question1 (solution to part 1-ii)
: 0:12:56 mins
-
6 - question2( recalls on question 2a)
: 0:42:37 mins
-
7 - question2 (solution to part 2a)
: 0:01:48 mins
-
8 - question2( recalls on question 2b)
: 0:24:28 mins
-
9 - question2( solution to question 2ii)
: 0:08:31 mins
-
10 - question3(recalls on question 3 parti)
: 0:22:21 mins
-
11 - question3(solution to part i)
: 0:05:14 mins
-
12 - question3(recalls on part ii)
: 0:11:45 mins
-
13 - question3(solution to part ii)
: 0:07:09 mins
-
14 - question4(recalls on part i)
: 0:32:00 mins
-
15 - question4(recalls on part i : integration)
: 0:13:09 mins
-
16 - question4(solution to part i)
: 0:10:17 mins
-
17 - question4 (solution to part ii)
: 0:05:12 mins
-
18 - question4(solution to part iii)
: 0:02:10 mins
-
19 - question5(recalls on circles)
: 0:18:04 mins
-
21 - question5(solution to 5b part 1)
: 0:20:20 mins
-
22 - question5( recalls on functions)
: 0:07:49 mins
-
23 - question5(solution to 5b part2)
: 0:10:21 mins
-
24 - question6 (solution 6 part ii(a))
: 0:05:54 mins
-
25 - question6(solution to part(ii)-b)
: 0:11:01 mins
-
26 - question7 (recalls on matrices)
: 0:36:21 mins
-
27 - question7( solution to part i)
: 0:08:47 mins
-
28 - question7 (solution to part ii)
: 0:05:39 mins
-
29 - question8(recalls on sequences and series)
: 0:13:56 mins
-
30 - question8(solution to part i)
: 0:04:05 mins
-
31 - question8 (solution to part ii)
: 0:04:10 mins
-
32 - question9(recalls)
: 0:06:02 mins
-
33 - question9(solution to part i)
: 0:15:42 mins
-
34 - question9 (recalls on binary relations)
: 0:03:35 mins
-
35 - question9(solution to part ii)
: 0:03:58 mins
-
36 - question10 (Basic recalls)
: 0:08:58 mins
-
37 - question10(Solution to part i-a)
: 0:06:15 mins
-
38 - question10 (solution to part i-B)
: 0:08:04 mins
-
39 - question 10 (recalls on complex numbers)
: 0:13:30 mins
-
40 - question10(solution to part ii)
: 0:03:16 mins
View PDF Notes
Take Quiz
Introduction
Pure Math Mech June 2020 Paper 2 Solutions




help 2 and 3
Hello kemba Ur solution will be ready by 6pm. Thanks
good luck foir maths
revise for the mock with this question
Question 12
The horizontal distance between two men P and Q is 6 m. A ball is projected by P to Q with an initial speed of 10 ms-1. Q catches the ball at a point vertically above him and at a height 3 m above the point of projection. Show that there are two possible angles of projection and find the time of flight in eac case (take g as 10 ms-2).
Solution
Diagramatic interpretation
Showing that there are two possible angles of projection
At point A where Q catches the ball,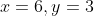
Substituting in the above equation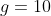 and
and 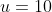 we have:
we have:
For us to have two values of the projection angle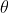 , we must have two values for
, we must have two values for 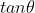 .
.
For us to have two values of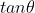 , the above quadratic equation in
, the above quadratic equation in 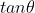 must have two real and distinct roots. In other terms, the discriminant must be strictly positive
must have two real and distinct roots. In other terms, the discriminant must be strictly positive
Therefore, for two angles of projection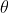 to exist, the discriminant of the above equation must be strictly positive.
to exist, the discriminant of the above equation must be strictly positive.
Discriminant,
Since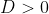 , there exist two possible angles of projection.
, there exist two possible angles of projection.
Finding the time of flight in each case
The solution of the above equation in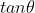 is given by:
is given by:
Using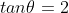 ,
, 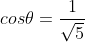
Substituting in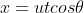 above we have
above we have 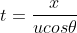
So time of flight in seconds in this case is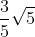
Using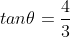 ,
, 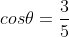
Substituting in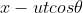 above, we have
above, we have 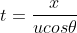
So time of flight in seconds in this this case is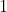
pleasw help number 13 and 12
Helloooooooo Good morning and hope you are doing well this is really a very long question to answer here may I know exactly the difficulties you face answering the questions or if you can snap what you tried doing so that we point out the mistakes it will be great
Follow the solution above
Any question and submit
A smooth sphere A of mass 3m is moving with speed 5U on a smooth floor. It's collides directly with another sphere 3U. Given that the coefficient of friction is ¼
Find
A. Velocity of the spheres after impact
B. The loss in K.E due to the impact
actually the question lack enough information like: mass of the sphere with speed 3u was the sphere with speed 3u was moving in which direction?
trig tutorials